Statistika adalah cabang ilmu yang berkaitan dengan pengolahan data, mulai dari perencanaan, pengumpulan, interprestasi, hingga penjelasan mengenai sebuah data.
Data hasil penelitian dikatakan valid apabila sudah dianalisa menurut aturan dan prinsip ilmu statistika.
Berbagai macam jenis penelitian baik di bidang sosial maupun eksak dan agro menggunakan statistika untuk merancang metodologi penelitian. Perhitungan-perhitungan statistika akan menghasilkan data yang diyakini tingkat kebenaran menggunakan metode analisis tertentu.
Dalam sebuah proposal penelitian statistika bermanfaat untuk merancang jalannya sebuah penelitian. Mulai dari preparasi, cara mengambil dan mengumpulkan data, hingga bagaimana menemukan kesimpulan dari hasil yang diperoleh.
Analisis Regresi Linear Sederhana
Dalam sebuah penelitian dikenal adanya variabel bebas (independen/ predictor) dan variabel tak bebas (dependen/ response). Uji regresi dapat digunakan untuk mengetahui hubungan atau pengaruh variabel bebas terhadap variabel tidak bebas.
Analisis regresi adalah analisis statistik yang mempelajari hubungan antara variabel yang diterangkan dengan variabel yang menerangkan.
Dalam model regresi variabel independen (bebas) menerangkan variabel dependennya. Dalam hal ini diasumsikan berlakunya hubungan linear dalam setiap parameter.
Disebut sebagai analisis regresi linear sederhana karena hanya terdiri dari satu variabel bebas (independent variable). Artinya variabel tidak bebas (dependent variable) hanya dipengaruhi oleh oleh satu variabel saja.
Apabila variabel bebasnya lebih dari satu maka analisa regresinya disebut sebagai regresi linear berganda. Artinya terdapat banyak variabel bebas yang mempengaruhi variabel tidak bebas .
Analisis regresi ini merupakan uji yang paling banyak digunakan dalam perhitungan hasil penelitian. Biasanya digunakan sebagai penentu akhir untuk menulis sebuah kesimpulan, apakah penelitian tersebut dikatakan berhasil atau tidak.
Analisis regresi mencakup beberapa metode perhitungan statistika seperti uji signifikansi (beda nyata) menggunakan uji-t atau uji-F, ANOVA, dan penentuan hipotesis.
Dari hasil analisis ini akan diperoleh persamaan regresi yang berfungsi sebagai prediksi pengaruh variabel terhadap variabel lainnya.
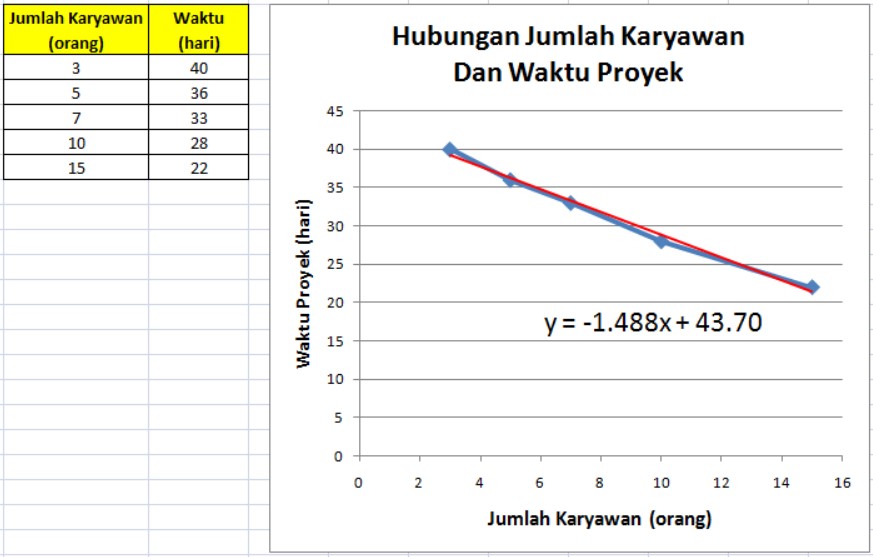
Secara matematik persamaan regresi linear sederhana digambarkan dengan garis lurus (linear). Merupakan model persamaan yang menggambarkan hubungan antara variabel bebas (X) dalam mempengaruhi variabel tidak bebas (Y), dirumuskan sebagai Y = a + bX.
Y = garis regresi yang dikenal dengan istilah variable response a = perpotongan sumbu vertikal (intersep), konstanta b = konstanta regresi (slope) atau koefisien arah/ koefisien beta X = variabel bebas (predictor)
Rumus tersebut menggambarkan hubungan linear yang artinya perubahan pada variabel X akan diikuti oleh perubahan variable Y secara tetap.
Apabila yang terjadi justru sebaliknya, dimana perubahan variabel X tidak diikuti oleh variabel Y maka hubungan tersebut tidak bersifat linear.
Asumsi-Asumsi Dalam Regresi Linear Sederhana
Secara sederhana berikut beberapa syarat yang harus dipenuhi apabila ingin menggunakan analisis regresi linear sederhana dalam uji statistika:
- Jumlah sampel yang digunakan dalam penelitian harus sama
- Hanya bisa menganalisa uji dengan satu variabel bebas (X)
- Data harus dalam bentul normal, artinya nilai residual harus berdistribusi normal
- Hubungan antara variabel bebas (X) dan variabel tidak bebas (Y) haruslah linear
- Tidak terjadi gejala heteroskedastistas dan autokorelasi (untuk tipe data time series)
Data time series adalah data yang disusun berdasarkan urutan waktu yang bisa memunculkan asumsi autokorelasi. Sebuah asumsi melihat pengaruh variabel lag waktu terhadap variabel Y. Artinya terdapat pengaruh variable lag waktu sebelumnya terhadap variabel tidak bebas (Y).
Dalam memperoleh hasil analisis regresi linear sederhana asumsi eksogenitas. Yaitu nilai error atau kesalahan pada variabel tidak tetap (Y). dimana disyaratkan variabel Y bersifat random, sehingga eksogenitasnya harus lemah.
Varians error (homoskedastistas) harus konstan, artinya nilai residual tidak berubah-ubah meskipun pada respon yang berbeda. Sehingga gejala heteroskedastistas harus dihindari agar tidak mengganggu model persamaan linear yang terbentuk.
Demikian penjelasan kami mengenai Analisis Regresi Linear Sederhana. Semoga bermanfaat.